Hello there!
This blog of F# contains full (long) blog posts of adventure in functional programming and F#. I call it adventure, because I’ll try to make F# as fun to as possible to learn.
NOTE:
This blog is starting to use Visual Studio from Visual Studio 2012 and Visual Studio 2013 (from Release Candidate to RTM), and provide hints of F# 3.0 in Visual Studio 2012.
Now, here are the parts:
- Part 1: Introduction to Functional Programming
- Part 2: Functional Programming Concepts (you are here)
- Part 3: Introduction to F#
- Part 4: Functions, Delegates and Computation expressions in F#
- Part 5: F# standard libraries
- Part 6: OOP in F#
- Part 7: Using LINQ in F# (and the upcoming F# 3.0)
- Part 8: F# Asynchronous workflow
- Part 9: F# MailboxProcessor
- Part 10: Units of Measures
- Part 11: F# Power Pack
- Part 12: F# for Silverlight 4 (and above)
- Part 13: A look at F# 3.0 in VS 11
- Part 14: A look of Functional Programming in VB 10 and C# 4.0 compared to F#
- Part 15: A look of F# compared to Haskell, Scala and Scheme
- Part 16: F# future and what features that F# must have
- Part 17: Retrospective
Functional Programming Concepts
Now it’s time to dive and discuss more of functional programming concepts. Again, functional programming has a very long history, but as I already said in part 1, you are already used it everyday (especially when you’re a Microsoft .NET developer).
A nice sample of everyday functional programming: Microsoft Excel!
Why? Microsoft Excel’s formula is always a “pure function”, once you fill the formula, the result will always be the same.
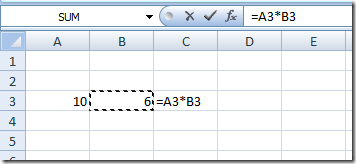
Try this in Excel:
In the cell C3, we see formula of “A3 * B3”. Once we fill in the formula, we can be sure 100% it will always return the same result no matter how many times you call the formula. Excel’s formula then also can be said as function as data. Because then you can pass the formula to other cell. This concept is called “function is first class” and there’s no difference of function and data.
Sidenote on function = data:
This can make most of us confused, because the nature mindset of common OOP programmers always separate functions (operations in OOP) and data. It’s different from the famous work of Nicklaus Wirth in “Algorithm + Data Structures = Program”. But I personally recommend to buy this book, because it’s still a very important resource for software developers.
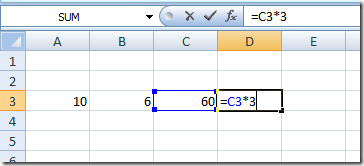
Why is there no difference? The content of formula in C3 can be regarded as data to be passed to other operations/formulas in other cells, just like this:
So we are already familiar with Excel, and I’m sure many of us are using it everyday! I can also safely say, Excel is the most used functional programming!
To make our adventure to be more fun, this Excel sample is the most understandable sample but then again, let’s go back to our developer domain, the codes and the concepts.
Why do I bring the concept first? Please walk the path, apprentice.
The journey of thousand miles begin with a single step.
- Sun Tzu
Let’s begin with the first mile, shall we?
What makes a functional programming language?
A functional programming language is simply programming with math functions. A function is simple: an operation that takes parameter and (must) return a result.
Then again this operation in math usually always return the same result.
First of all, functional programming always take at least a parameter and return a result.
These are the concepts that really makes it shine:
- Function as first class citizen
- Fun with Currying in functions and introduction to tuples
- Higher order functions
- Pure functions
- Recursions (recursive operations)
- Type inference
- Strict (eager) evaluation versus non strict (lazy) evaluation
Let’s dive into #1 to #6 first in detail and #7 in short overview. I’ll discuss #7 details on part 3, because this topic is dealing on the nature how F# evaluate expressions in functions.
Function as first class citizen
On the entry of first class function on wikipedia, it means that language supports to pass functions as arguments (parameters) to other functions. But this functions as first class citizens isn’t just this, it also means that functions and data structure has no difference.
This matter is nicely wrapped in MSDN Library documentation on F# about F#’s first class functions:
Typical measures of first-class status include the following:
- Can you bind an identifier to the value? That is, can you give it a name?
- Can you store the value in a data structure, such as a list?
- Can you pass the value as an argument in a function call?
- Can you return the value as the value of a function call?
You can check the MSDN Library first and then try to understand what are those concept with the samples provided, but I myself can’t simply grab the concept at first.
A word of notification of this part sidenote:
I’m not simply copying and pasting from MSDN Library. Some of the words and sentences in MSDN Library is quite hard to understand at first, but always make your precious MSDN Library documentation as your first source of information, because it’s the official way to get information about .NET and also .NET programming language family from Microsoft. This blog entry will try to provide you easier way to understand what is on the MSDN LIbrary description about F# first class functions.
For the next parts, I will keep quoting MSDN Library and always give more simpler definitions and with samples.
About why there are more capture of VS 2010 F# Interactive?
Begins with this part, I prefer more to give you a captures of VS 2010 IDE and F# Interactive.
My main goal is to show you the type signature and the resulted output of F# Interactive, rather than going thru full IDE and debug. By seeing the result and the type signature, you will have more understanding of functional programming power features such as currying.
Also this will give us immediate results to know and to test what’s our code doing. This distinguish F# feature is the distinctive feature that looks like other kinds of dynamic languages such as Python and Ruby but C# and VB.NET currently doesn’t have it yet. Again, the F# interactive can be considered as also REPL capability of F#! More sample of this interactive scripting? Follow the rest of this part, guys.
From the four measures, the last two are the main traits of “higher-order function” according to MSDN Library:
The last two measures define what are known as higher-order operations or higher-order functions. Higher-order functions accept functions as arguments and return functions as the value of function calls. These operations support such mainstays of functional programming as mapping functions and composition of functions.
Keep in mind for now about the higher-order function matter “mention” from MSDN. But the content only said that, not further explaining about what “higher-order function” really means.
More on what is higher-order function? Later also in this part. But let’s walk thru those four questions of first class citizen thing.
Bind identifier to the value
Common in functional programming, the act of assigning value to an identifier is “binding”. This value assignment is different from value assignment of OOP, which value can be modified later and also can be modified many times.
Once you bind the value, it can’t be changed.
Functions in functional programming can be represented by a function symbol such as f(x) or also by a defined symbol such as y.
f(x) = y
by then, y can be considered as symbolic variable of f(x), not just the result. Again, this is different from the OOP we used to have, that y is only the result of the operation.
The function value itself can be an operation like this:
Yes, squareIt is a function that contains operation that needs parameter (argument) n, the operation is “n * n”.
F# then can make the syntax above shorter without “fun” keyword:
let squareIt n = n * n
The function is named “squareIt”.
Store the value in other data structure such as list
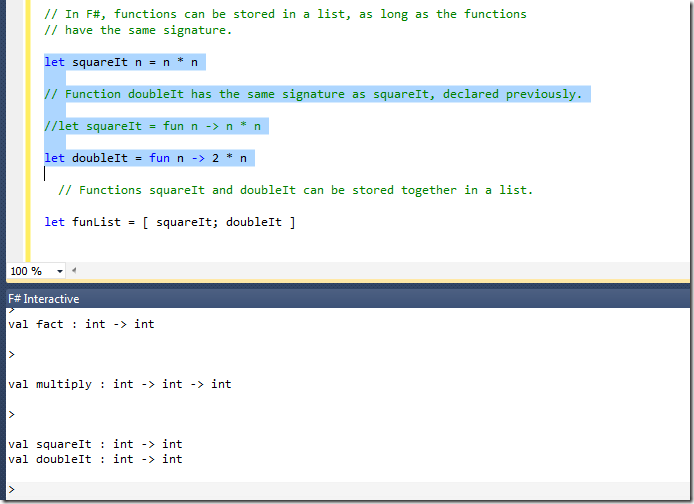
Using the squareIt above, we can create a list of functions in a list (or collections in .NET).
But first, let’s create a function called doubleIt:
let doubleIt = fun n –> 2 * n
If we want to create a list that has squareIt and doubleIt, we have to be sure that they must have the same signature.
Because squareIt and doubleIt already has the same signature, we can create the list that has them, like this below:
The function signature of doubleIt and squareIt is the same:
As you can see above, the signature is “int –> int”.
This means it takes a single argument with type Int32 and returns an Int32 value. Why? Because F# (and so other functional programming language such as Haskell and Lisp) has type inference built in, and it’s by default give Int32 as its type. More on type inference later.
For those .NET developers, we all know we have Delegates that represents a function. But functional programming takes it further: it also supports pairs of tuples as parameter, if the argument is more than one. More than one? see Fun in currying in functions topic later.
Pass the value as an argument
If the value has first class status, you can pass it as an argument in other function.
For example:
The symbol “greeting” has “Hello” as its value. We often see this in other languages, including non functional such as VB and C#.
What about functions?
MSDN Library said this:
If functions have first-class status, you must be able to pass them as arguments in the same way. Remember that this is the first characteristic of higher-order functions.
Yes, we must have the abilities to pass function as arguments of a function as well. This “in the same way” means in the same way as we treat data/value that passed as an argument to a function.
MSDN Library has this as a sample:
But unfortunately, the sample above is including sample of a higher order function that’s composed from combining or chaining functions.
Why? Because most functional programming families can return a function, not just having function as argument.
Look at the applyIt:
let applyIt = fun op arg –> op arg
The applyIt function is equal to a lambda that take an op and arg, and it returns a function that takes op returns an arg.
The function applyIt2 has the same meaning of the applyIt above.
But to be honest, do you find it’s easier to read and understand? Not for me.
Want more on this but in a simpler? Please see “Fun with currying in functions and introduction to tuples” topic later.
Return the value from a function call
This is the last trait of “functions as first class citizens” but it’s also important: function can be returned from a function call (as a return value).
Let’s start with a simple sample. Usually, a function returns a value that is simply a result value of a simple type, either primitive or a complex object. This is also known available in other programming languages as well, not just functional.
Simple function like this:
let multiply a b = a * b
will return a result of a x b.
But functional programming takes it further: it can return a function.
MSDN Library emphasize it:
The ability to return a function as the value of a function call is the second characteristic of higher-order functions.
Let’s look at MSDN Library again and put the sample into code in VS 2010:
First, we have checkFor function with item as parameter. I haven’t give the type for the parameter, but because the code body of checkFor is including the call to List.exists, then the type of returned function of “functionToReturn” is “ list –> bool “. This happens because List.exists return bool.
The type of “item” argument is further checked because there is a comparison of equality in the body of a lambda function of “(fun a –> a = item)”. Therefore type inference in F# will also mark the “item” argument has to have implementation of equality in F# (almost analogous with IEquatable and IComparable in .NET).
This mark is noted with “when” keyword to mark as a constraint.
Another thing is: item is then safely assumed to be generic as long as it can have equality operation.
This is also a sample of powerful of type inference in F# in action! More on type inference later in this part.
This other sample from MSDN is slightly more complex but with comments:
Sample above also features heavy currying. Move on next: have fun with currying and tuples!
Fun with currying in functions and in introduction to tuples
Any functional programming languages family have the ability to currying and use tuples. Both of these concepts are so powerful and convenient, not to mention it’s also helpful to ease complex operations in composite functions.
Also the use of tuples makes writing functions and manipulating it more fun!
In part 1, I have shown you the recursive Fibonacci function. In the F# interactive below, you’ll see the type signature of the function (not just the type of the parameter.
Sidenote on F# interactive:
You may wonder what really F# interactive is. It is a “wrapper window” to host F# Interactive prompt. F# Interactive itself is a command line executable to perform directly REPL (Read Eval Print Loop) interpreter of F#. It has its own call stack because it can remember function definitions.
You don’t have to know all about REPL, but if you want to know more, visit the CommonLisp tutorial at http://www.gigamonkeys.com/book/lather-rinse-repeat-a-tour-of-the-repl.html for more detailed information and samples.
The signature of function fact is:
fact : int –> int
means it takes argument with integer type, and returns a result of integer.
What happens if I give multiple arguments?
For example, I want to have function that multiplies a and b, I can write this:
let multiply a b = a * b
using F# interactive, I can check the type signature:
Yes, it may confuse all of us. But it’s simple: it takes an argument of int, passed as function that needs an argument of int, then return an integer.
Functional programming languages especially Lisp, ML language family and Miranda knows this well as implementation of Currying.
ML language family (including F#) has tuples, not just using currying as parameter.
Let’s do currying!
What is currying? The term currying has a very long history. It was taken from the name of Haskell Curry, a famous American mathematician. Haskell language itself also from the name of Haskell Curry. Neat!
The base theory of currying is from combinatory logic. It is basically how to compose and compose chain of functions (as long as the return value is the same type). Although it’s part of computer science, it’s actually part of mathematics especially calculus and mathematics’ logic.
Currying takes from Lambda calculus discipline. It’s a way to transform multiple arguments of a function then turn it into a chain of function arguments.
For example:
multiply int –> int –> int
is the same as
multiply(int) –> (int –> int)
the longer meaning is: function multiply takes a and return a function that takes b and return c. In other hand, I can replace second parameter with function that has int –> int as signature.
So, I can write other function as parameter to multiply:
And the code will display 30, as a result of 5 * 6, where 5 multiplier comes from multiply5 function.
Try to do this in other languages such as C# and VB? You can’t. There’s no syntax support for this.
Sidenote on multiply sample:
Actually, this sample comes from a question in Stackoverflow that asked about currying in F#. I was learning from this question too.
As a matter of fact, this is why I said earlier that MSDN Library is not clear enough to explain the concept of functional programming especially on function currying, even though it has samples, like the one about the function of applyIt2 before. This is why I have to look elsewhere.
Therefore, let’s see this sample again:
f(x –> y –> z) = f(x –> (y –> z))
Then the currying has to be right associative. For more than 3 arguments:
f(a –> b –> c –> d) = f(a –> (b –> c –> d)) = f(a –> (b-> (c -> d)))
It is always pushed toward the rightmost expression first. So in the sample below, this expression on the right is wrong in currying:
f(a –> b –> c-> d) <> f(a –> (b –>c) –>d) // <- THIS IS WRONG! It is not equal.
There’s also number of samples to do this in C# and VB, but it’s with the help of partial function application concept and full use of lambda expressions.
Not just using common curried functions, ML family languages have the ability to use Tuples as arguments.
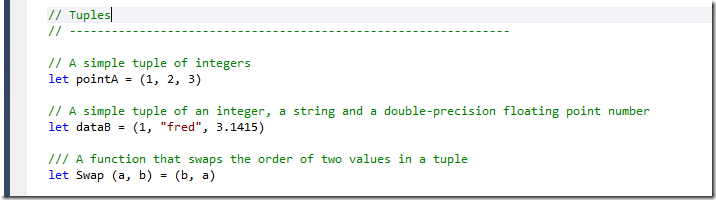
Meet the tuples
In the sample tutorial from Visual F# “F# Tutorial” project templates, you will find many simple samples. Just add new project to an opened solution like this picture below:
In the sample, you’ll see this:
Basically a tuple is a list of unnamed but ordered elements or values. It is unnamed, but it is ordered in the order of values given. This will also determine the type of the tuple.
The sample above is then translated into this:
This is why it’s called ordered elements instead of just elements, because the order is important.
If you define the tuple as (1, 2, 3) then the signature is “int * int * int” and this means that the first element is int, second element is int, third element is int.
The value of dataB is typed as “int * string * float” and this means that the first element is int, second element is string, third element is float.
The Swap is a function that takes tuple as its arguments, and the return value is a tuple with different order of elements. But swap itself is a sample of a curried function with a single argument, as you can see the “->” in the signature of “ ‘a * ‘b –> ‘b * ‘a ”. The “ ‘a “ and “ ‘b “ in F# means that it’s inferred as generic type.
It’s quite powerful to combine currying with tuples! This is why I called I have fun using currying and tuples.
Please don’t confuse the “*” in the signature, it doesn’t mean multiplications at all.
Sidenote on tuples:
Tuple in F# was not available in .NET before .NET 4.0, although tuples in F# has been available from first release of F#.
Fortunately for us, F# tuples is now a part of .NET 4.0 and of course will also be available in .NET future releases. More on Tuple? Later on “Part 3: Introduction to F#”.
Wait, there’s more! Because function is also a value in functional programming, we can also make tuple but the elements can be typed as functions. Again, also on Part 3.
Higher-order functions
A higher-order function is simple. It is simply a function that takes other one or more functions as its arguments and then return a function. As explained earlier, these are two traits of functions as first class.
I have already provided samples in F#, but I bet many of us are still juggling in C# or VB (or both if you’re a polyglot like me)
The easiest sample is by investigating how .NET 3.5 (and above) LINQ’s “select” work. A select in SQL is simply a projection, that map each element in a list to other element in other list. Therefore it can be considered as map function.
Sidenote on map or projection:
This map is relatively the same as Map in MapReduce, the popular algorithm invented by Google to scale massive dataset processing.
This “select” projection in LINQ is very easy to understand, as it takes delegate of Func<TSource,TResult> that performs operation on each element to be projected. Most of the other SQL clause such as WHERE and ORDER BY are also implemented to take delegate as parameter.
Let’s look at the Select method signature in C#:
public static IEnumerable<TResult> Select<TSource, TResult>(
this IEnumerable<TSource> source,
Func<TSource, TResult> selector
)
In the signature, the function is included as parameter.
Sidenote on extension method:
The this marker on first parameter signifies that this method is an extension method of IEnumerable<T>, or you can make extension method with <Extension> attribute in VB, due to the difference on how the compiler work in C# and VB.
Also starting from this part, I will encourage you my dear readers, to be a real polyglot software developers, not just being coupled to one or two programming languages and also not just using them.
Inside the body of the select, this is the code: (because TSource and TResult are generics, I can simply replace them with T and U)
Yes, it takes delegate as functions to operate on each element.
What about map? Map in F# has this signature:
It has the same effect as Select in LINQ, but it uses curried syntax and semantic.
As a matter of fact, SQL queries of SELECTs are samples of (partial) functional programming in action by looking at how LINQ is implemented. An entry of functional programming in Wikipedia also states this. But LINQ goes further, because the nature of .NET that it can returns delegate, hence function as the result.
I said partial, because the original SQL SELECT cannot return operations, only returns a list of data or a simple scalar value.
For more fact on why SQL SELECT is functional, you can do this:
- Perform a subqueries on WHERE clause, not just simple conditional clause such as “Employee.PK IS NULL”.
- Perform nested SELECT. The nested select itself is a sample of operation as parameter.
- The returned result of subqueries is immutable, you can’t modify it again. To modify it, you have to make assignment to other variable or alias to other name.
This ability comply with the trait that we can pass function as argument. The data returned on SQL is simply a list, therefore it doesn’t satisfy a second trait, the returned result can be a function result.
Why do we call it “higher-order”? Because the function that has functions as arguments has higher order of the way we look and analyze the function, therefore it has higher abstraction. Other function such as Sin(X) is simply a first-order function.
The concept of higher-order functions are also useful in function compositions.
We are familiar with this notation:
The left hand expression reads “f circle g”. Function f is called higher-order function, and function g is called first-order function.
For example:
f(x) = x ^ 2
g(x) = x + 3
so,
f(g(x)) = f((g(x) ^2)
We can “open” the parentheses in the right hand expression and then make it more natural in order of operation:
f(g(x)) = g(x) ^ 2) => (x + 3) ^ 2
in F#, we can simply do this: (the exponentiation operator in F# is “**”)
If I call f_circle_g 5.0 the result is 64, because:
f(g(5)) = (5 + 3) ^ 2 = 8 ^ 2 = 64
It’s more succinct, and it’s a proof that every function in F# is higher-order function. Can we do this in C# or VB with less noise?
As in the law of math, f(g(x)) is not equal to g(f(x)).
Proof: modify the code above to do this:
let g _circle_f = g << f
and see it.
Pure functions
Pure function means a function that will always return the same result (as long as the argument has the same value) no matter how many times we call it. Therefore it shouldn’t have side effects that may be affecting the result of the function.
This side effect is including error exceptions, I/O access, or any state affecting the output of the result.
For example:
let f x = x * 2
this function is a pure function. No matter how many times you call it with the same argument value, it will return the same.
A call of f(2) will always return 4.
But if we call a function that returns current date and time, it’s not a pure function, because it will always return the latest date and time.
To simplify this, look at this F# example:
This anytime function will return the latest time, but every time we call anytime, it will return different result. Therefore anytime is not pure.
This flexibility in F# also means that F# itself is not a purely functional programming language, because F# is able to mix pure and non-pure (impure) functions and operations. F# itself (and so other OCaml language family) still accept exception handling as part of its features.
Next, one of the important aspect of a functional programming: recursions.
Recursions (recursive operations)
A recursion is simple: an operation that execute the operation itself. Put it simply in a context of functional programming and imperative programming: a recursion is an implementation of a function that called itself.
Recursion has its roots in computer science. Wikipedia said:
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem.[1] The approach can be applied to many types of problems, and is one of the central ideas of computer science.
The [1] note mark points to chapter 1: Recurrent Problems of “Concrete Mathematics” book by Donald Knuth, Ronald Graham, Oren Patashnik. Personally I would not recommend this book as a reference, because it’s not quite easy for me (and some of my close friend such as Nicko). It might be easy to understand for those that has backgrounds in math or pure computer science.
Sidenote on Computer Science mentioned in this series of F#:
Please don’t mix Computer Science with Software Engineering. Many large companies and most universities in Indonesia often mix these as the same discipline, but it’s not the same in nature and in curricula. Computer Science deals with the science of computation and raw programming language theories including discrete math, automata, compiler, and basic calculus. Software Engineering deals with how to develop software (including methodologies such as waterfall and iterative) with only a small portion of introduction to common programming language (such as C++) and OOP.
It really hurts my professionalism and my common sense as a real polyglot software developer. Unfortunately, this misunderstandings continues.
A good sample is the list of courses from RMIT Australia: http://www.rmit.edu.au/browse/Study%20at%20RMIT/Types%20of%20study/Degrees/Computing%20and%20information%20technology/
More on this (and also polyglot) on part 17, Retrospective.
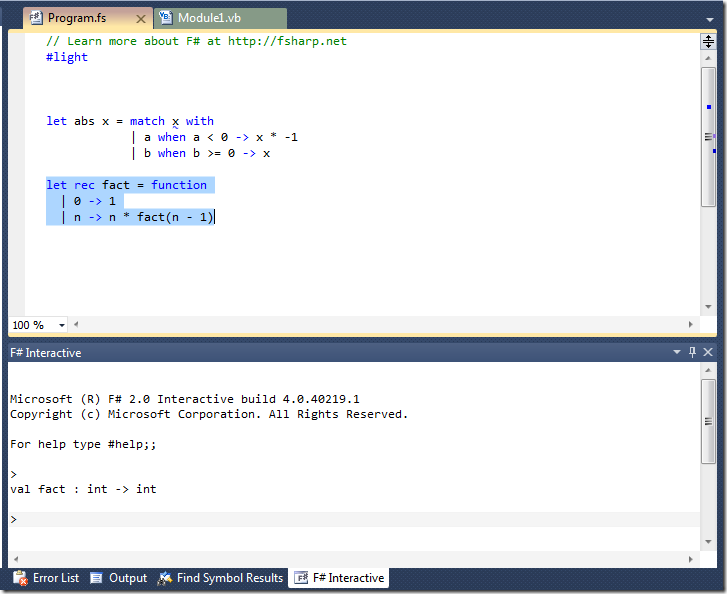
Let’s revisit the factorial sample from part 1:
We can see that fact function is recursive by looking at the function body. And by looking at the “pattern” of “0 –> 1”, you can also see that there’s a limit of execution. It will stop when the argument is equal to 9, because it will immediately return 1 as a result of fact(0) and it’s also the same as the math equivalent:
0! = 1
To create a recursive function, IBM Developerworks has nicely summarized it:
- Initialize the algorithm. Recursive programs often need a seed value to start with. This is accomplished either by using a parameter passed to the function or by providing a gateway function that is nonrecursive but that sets up the seed values for the recursive calculation.
- Check to see whether the current value(s) being processed match the base case. If so, process and return the value.
- Redefine the answer in terms of a smaller or simpler sub-problem or sub-problems.
- Run the algorithm on the sub-problem.
- Combine the results in the formulation of the answer.
- Return the results.
The base case in point #2 is the “final escape” to immediately return a value or stop, instead of infinitely calling the function again. This is often called a “limit” or “boundary condition” which the recursive function must have.
The point #3 is very challenging: we must identify the problems into smaller sub problems that has the same way to solve as identified in point #4.
For more info, visit the link at the end of this part.
As a consequence of calling the same function inside the function’s body, the runtime needs to keep a location to remember where the self calling execution start, in order to gracefully return to previous caller. Therefore a recursive function can be dangerous to run if it’s ran many times without checking the limit of available stacks, therefore most programming languages will give error quite similar as “Stack overflow”. This indicates that the code is using all of available stacks and running out of them.
Yes, we can write factorial in a more verbose such as this in VB.NET:
Now you have it, although it’s noisier. The base case is if x = 0 then return 1, the simpler problem is after “Else”.
Hint sidenote:
Try create a factorial in C# or VB.NET like that sample above and execute the factorial function with very large number such as 50000. And see for your self what happened.
If you have smaller argument value such as 10000, the code will not catch exceptions/errors, but the result may vary. The code will result a value larger than Int32, therefore larger integer needed to store it.
In the case of VB.NET 10, the console will output "”Infinity”. In C#, it display 0. I’ll leave it to you why is this different.
There are more behavioral differences to this than simple C# and VB.NET. Microsoft has done many things in bringing these two language closer, but there are still more glitches. Why should you care? Because not many of us are just C# or just VB developer.
In most common functional programming language, this stack overflow can’t occur if the compiler is smart enough to know that it can be compiled using “tail call recursion optimization” as long as the platform infrastructure allows it.
Tail call is simply a function that its result is immediately used as the output of the function. F# compiler is smart enough to know what is recursion or not with the help of rec keyword. More on tail call on part 3.
But our F# factorial is still not quite a good sample, because a limitation of Int32 type length in .NET. Also if you use Int64, it will be limited. You can also use
Then why recursion is part of functional programming traits? I’m curious, and you should be.
Because the answer lies in the nature of how we describe math functions when we perform factorial loops in math: it can be represented recursively, not just iterative that is normal and the default way in imperative.
Let’s revisit factorial in piecewise notation:
If we focused in using the recursive, it’s more natural and it’s easier to understand than using the iterative notation of single capital Greek “PI”. The use of recursive in our code will also benefit more, because there’s minimal risk of changing internal values and also minimize or avoid the use of mutable value.
To return value, simply call the function again until it reaches the limit or boundary condition.
Type inference
Type inference is a feature of interpreting the type system of any variable used without specifying the complete type name. The type system will automatically set default type depends on any value used, but there are some conditions to be taken care of.
Those of you that already used Visual Studio 2008 and .NET 3.5 will recall that C# and VB has heavy uses of this in LINQ, and many of you may guess that this .NET 3.5 is the first version of type inference introduced in our .NET programming family. Is it right?
You are definitely wrong.
In .NET 2.0, C# 2.0 already has it. And you can see it in action on the code of Select before (without the this keyword on method parameter). The code above will work smoothly on .NET 2.0. Why?
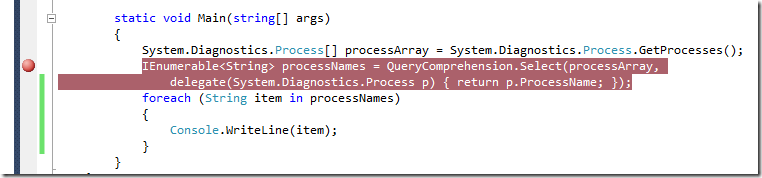
Let’s revisit the Select code and dissect it: (I have modified the var and replace it with T, and wrap this method in a static class named “QueryComprehension”)
Now test the code using this simple sample:
Display any running process and map it to just process name:
As you see, the GetProcessses() returns an array of Process.
This is then can be used as an argument as IEnumerable<Process> because an array of Process is also implicitly implements IEnumerable<Process>. Then the T is typed Process. The anonymous delegate will also infer <Process, String>based on the return type of ProcessName which is also String, then wrap it up in an IEnumerable because of the yield iterator.
But F# has gone further, the type inference is flowing thru the code, and it’s also flows in the curried functions. This technique is known in other ML language family, based on the work of Hindley and Milner.
The type inference of F# used is typed lambda calculus.
Sidenote on lambda and calculus mentions:
Lambda calculus is taught in computer science, not just in pure Mathematics. But if you follow my explanations and always check MSDN Library, I’m sure that you will understand why it’s very important to know some aspect of real computer science, not just using the implementation of it in day to day software development.
Other concept of side effects, lambda, and then Monad in the next part may hurt your head to learn it, but please bear with me because they are inescapable properties of functional programming.
The work of Hindley and Milner was later enhanced and formalized, thanks to the work of Luis Damas.
ML language family used typed lambda calculus instead of untyped lambda calculus. Why typed lambda instead of the opposite, the untyped?
Before we dive into this, let’s have a quick visit to the basic theory of what a programming language is made of.
A programming language usually must satisfy this:
- Turing complete
- Has data structure, therefore has to have type system
- Has reasoning about how the code will be parsed and compiled
A Turing complete means the programming language must be able to simulate other general purpose computer and/or programming language within the limit of finite memory and therefore, linear bounded automaton. If some of you have studied Informatic Engineering (a.k.a. Teknik Informatika in Indonesia) then you are lucky, this is part of Compiler theory and Automata as subject. But I won’t dive into it now, because it’s part of Computer Science.
It must be, because its nature of explaining the essence of how programming language’s compiler works, not emphasizing on how you develop software application.
And so are the others: data structure, type system, and programming language reasoning.
Turing complete also means that a programming language should be able to do what other general purpose programming languages do, this includes doing looping, branching, and calculations of data, not just displaying output. As a consequence of this, a formal type system has to be defined to satisfy and to understand kinds of data to be processes.
Sidenote on type system:
At the end of this 17 parts of adventure, I will dive into “Type System” as part of my effort to simplify most of the basic theories of programing languages, the type system. This is including functional type system.
If you want to know more about type system than waiting for me to finish this article, I highly recommend you to read the one of the ultimate book of computer science, the TAPL book: “Types and Programming Language” by Benjamin Pierce. Although I personally don’t have background on computer science, I highly recommend you to buy and read this book.
Type system is put it simply: a set of rule for governing how types is interpreted and then further processed in a programming language. This rule include the static typing and dynamic typing programming languages.
Static typing means the type must be defined and the typing is constant. For example, once you defined a variable as Int32, then you will always bound the variable to be typed Int32 as long as the program runs.
Dynamic typing means the type can change at any time when needed, therefore the type declaration is not mandatory or even necessary. This typing is called dynamic, because it is not static all the time.
We used to know static type language such as C#, VB.NET, Java, F#, and all of the other functional programming languages including OCaml family, Miranda, Haskell.
Dynamic type languages are many; some of them are Javascript, Ruby, Python.
F# is static typed, so are C# and VB. Let’s see the samples.
We used to see this in C#:
String abc = “abc”;
Int32 a = 0;
or this in VB:
Dim abc As String = “abc”
Dim a As Integer = 0
But type inference in C# since C# 3.0 making it simple:
var abc = “abc”;
So type inference means deducing (or translating) the type, using dependency on the result value equation without declaring the full type before.
But ML languages such as F# goes further, for example:
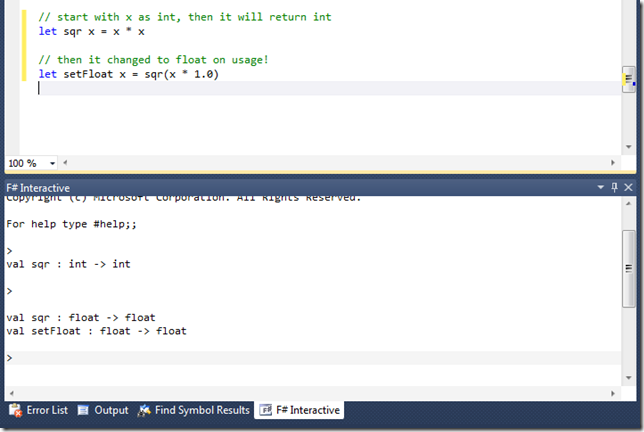
let sqr x = x * x
The type of x is default to Int32, therefore the return result of sqr(x) will be typed Int32 as well.
Try to do this in C# and VB? You can’t do type infer on the function declaration of return type of the function.
Now, add some new function and use float literal and see what happens next:
It’s incredibly powerful and creepy, isn’t it? Creepy, in a sense that the type will be inferred base on the expression of the next value/usage, although all of this will happen at compile time.
Not just F#, because type inference in all of the OCaml family includes type inference in functions and also in currying functions and tuples!
Also depends on how you write the functions and the operations, the type will be inferred according the operations.
Also F# when used in scripting or interactive will change the type inferred accordingly, based on the parameter usage of the function.
It doesn’t stop here; F# can also infers types and expressions using automatic generalizations. Again, VB and C# doesn’t have this yet, and neither other OCaml family language. I will dive more of this on Part 3 and Part 4.
Strict (eager) evaluation versus non strict (lazy) evaluation
The fact that it’s all about functions and expressions, it also brings more consequences that in order to fully guarantee immutability, the value of a function result has to be safe (will always return the same) because it’s pure. Therefore it can be later safely evaluated when needed. This is often called lazy evaluation
The opposite is eager evaluation, where function is eagerly evaluated immediately.
This is why functional programming languages are often divided into these kind of evaluation strategy.
Then how to see this in action? You can do it using debugger.
Using the C# previous code of Select, you can debug the code.
The code to test and mark the line to debug is here:
Now, run the code.
When the debugger reached the breakpoint, step into it. The execution flow will step to the foreach!
Step into it again, then the debugger will go to the body of the Select method and iterate the foreach.
This proves that lazy evaluation is in action, simply it will evaluate only if the IEnumerable is iterated. What about in F#? More on this on Part 3!
Further reference links
These are further links of part 2:
- Currying on Wikipedia, http://en.wikipedia.org/wiki/Currying
- Sample of fun with currying on Brian Mc Namara’s blog, http://lorgonblog.wordpress.com/2008/04/03/f-function-types-fun-with-tuples-and-currying/
- MapReduce tutorial from Google, http://code.google.com/edu/parallel/mapreduce-tutorial.html
- IBM Developerworks tutorial on “Mastering recursive programming”, http://www.ibm.com/developerworks/linux/library/l-recurs/index.html
- Coevolution of C# and VB as part of C# and VB future, a session of Luca Bolognese on PDC 2009: Future directions of C# and VB, http://channel9.msdn.com/Events/PDC/PDC09/FT11
- Hindley-Milner why is so cool? Daniel Spiewak explained it in a blog entry: http://www.codecommit.com/blog/scala/what-is-hindley-milner-and-why-is-it-cool
- F# automatic generalizations in MSDN Library: http://msdn.microsoft.com/en-us/library/dd233183.aspx











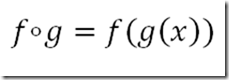









No comments:
Post a Comment