Hello there!
This blog of F# contains full (long) blog posts of adventure in functional programming and F#. I call it adventure, because I’ll try to make F# as fun to as possible to learn.
NOTE:
This blog is starting to use Visual Studio from Visual Studio 2012 and Visual Studio 2013 (from Release Candidate to RTM), and provide hints of F# 3.0 in Visual Studio 2012.
Now, here are the parts:
- Part 1: Introduction to Functional Programming
- Part 2: Functional Programming Concepts
- Part 3: Introduction to F#
- Part 4: Functions, Delegates and Computation expressions in F# (you are here)
- Part 5: F# standard libraries
- Part 6: OOP in F#
- Part 7: Using LINQ in F# (and the upcoming F# 3.0)
- Part 8: F# Asynchronous workflow
- Part 9: F# MailboxProcessor
- Part 10: Units of Measures
- Part 11: F# Power Pack
- Part 12: F# for Silverlight 4 (and above)
- Part 13: A look at F# 3.0 in VS 11 (Visual Studio 2012)
- Part 14: A look of Functional Programming in VB 10 and C# 4.0 compared to F#
- Part 15: A look of F# compared to Haskell, Scala and Scheme
- Part 16: F# future and what features that F# must have
- Part 17: Retrospective
Function, Delegates and Computation Workflow in F#
Before we dive deeper into this, please remember one thing: functional programming is programming with functions, just like mathematical functions. It doesn’t matter whether we are into pure functional or non pure functional.
Pure functional or non pure programming has to be able to handle side effects, and this is why Monad concept is so popular in functional programming languages. Therefore it’s useful to know Monad concept as well.
We are now learning the what the heart of functional programming is, the function. Only now let’s dive and focus on F#’s functions.
Functions in F#
In functional programming, there are no differences between data and functions, and functions can be passed as data. We already can pass function as arguments using delegates. But functions and delegates in F# are quite different from C# and VB delegates that usually uses Func<T>, Func <T,TResult> and the other larger amounts of Func parameters.
We have learned that in previous part 2 and part 3, functions in F# are special. They can be curried and then can be chained and also composed as higher order function, not just simple function that return a value.
The function itself can be treated as data, therefore can be passed as parameter to other function.
We already have this in .NET, under the name of Delegate. Because it’s on .NET, it’s available for other languages not just F#; delegates can be immediately used in C#, VB and managed C++.
Let’s make a function that has square operation:
let square x = x * x
The signature will be:
int –> int
Because there’s no type declared, the default will be Int32.
Now, using the function is simply calling the function with parameter, like this example:
square(5)
Of course the result is 5 x 5 = 25.
In F#, a function is curried (see previous part 2) and you will be able to chain it up and to create a higher order function.
Why do you have to care about the signature? Because this is the nature of F# function: it can be curried as well just like functions in part 2. Also it’s different from VB and C# when it has been compiled!
Before diving deeper, let’s dissect common F# code in a project (instead of using interactive mode).
By default, the common function declarations of F# exists in Modules, and these modules are simply the same as static classes in C# and Modules in VB. But declaring functions in F# is different.
Here is a sample of math module:
module MathModules
let sqr x = x * x
let rec simpleFactorial x =
if x = 0 then 1 else x * simpleFactorial x - 1
As we see, it’s simple.
Now, let’s dive into the source code of MathModules in C#: (using free JustDecompile from Telerik)

In the source in C# we can see that it has CompilationMapping attribute attached to it, and it’s simply to define the class as Module in F#. Without any modifier means that all functions in F# are public and static by default.
Again, the source decompiled in C# is longer than the one in F#, and it has many noises.
As described in previous parts (especially part 2 and part 3) if there’s no type signature in a simple arithmetic operation, the type will be inferred as integer.
What about multiple parameters?

Then the decompiled version will be:

Again, it’s different, and there is CompilationArgumentCounts attribute at the multiply function.
What is this attribute, really? Seeing this on MSD Library:

It means that this function accepts a partial application of some of its arguments. Now, when we have multiple parameter, then it can be curried as well!
Let’s recall this currying sample from Part 2:

Now, let’s incorporate those sample into our MathModules:

Now we have a higher-order function, it is “makeFactorOf3”.
And launch a decompiler tool to sneak in C#: (I have hidden the same sqr method to increase overall source code difference)

F# compiler has converted makeFactorOf3 to be typed as FSharpFunc<int,int>!
And the F# compiler generates new internal class of makeFactorOf3u004012 with code that has invocation of multiply. This is where the similarity between F# and other languages in Visual Studio break!
And you might wonder how to call this function from other languages such as C# and VB? Later on Part 14.
Now let’s explore F# functions and delegates deeper.
Returning value of function result
By looking at simpleFactorial function, we can have function body more than one line and also can have statements. But there’s one convention: the final line on the function body or the entire expression within the function body (including the statement) must evaluate into a value, and this value is the return value (or simply the result) of the function. Therefore, there’s no verbose return statement in F#.
But we must include indentation to signify that the function is indeed having many statements inside for functions that has many statements.
This concept will imply that we must evaluate value returned in a maintainable manner, as simple as possible!
This is different from C# and Visual Basic which can have return statement at any position! But this simple convention will give us more discipline that always has one point of return value, instead of having many return statement in our code.
What about using match (pattern matching) in F#? It is still evaluate to a value to be immediately returned as function result.
See this sample:
let defineQuality grade = match grade with
| "A" -> "Best"
| "B" -> "Very good"
| "C" -> "Good"
| "D" -> "Bad"
| _ -> "Undefined"
Compare it to C# code with the same functionality:
String defineQuality(String grade)
{
var qual = "";
switch (grade)
{
case "A":
{
qual = "Best"; break;
}
case "B":
{
qual = "Very good"; break;
}
case "C":
{
qual = "Very good"; break;
}
case "D":
{
qual = "Bad"; break;
}
default:
{
qual = "undefined";
break;
}
}
return qual;
}
Yes, we can enforce to make return statement in one position just like the code above.
But this will become obvious if we use if statement, just like this in C#:
String IsPositive(int anynum)
{
if (anynum>=0)
{
return "Positive";
}
else
{
return "Negative";
}
}
When I was leading a team of developers, I often found that code and when the inside if bracket the code contains another ifs and returns, the code will become hard to maintain and it’s still true until now! We will have two maintenance point of return values in that code above.
Now compare the code above in F#:
let IsPositive x = if x >= 0 then "Positive"
else "Negative"
It’s somehow quite a little bit hard to maintain but it still doesn’t violate F# convention to return value immediately. Now we can refine the function above into:
let IsPositiveV2 x =
let evalResult = if x>= 0 then "Positive" else "Negative"
evalResult
Now we can see that evalResult is acting as the return value of the result, and we must have indentations.
If you want to explicitly specify the type of the returned values, you have to group the parameter into parentheses.
For example:
let multiplyV2 (a) (b) : int = a * b
and multiplyV2 will have this signature:
val multiplyV2 : a:int -> b:int –> int
This brings another convention: the last type in a function signature means the result/return value type.
Writing parameters of a function
Now let’s dive deeper about parameters in a function in F#.
We already have “sqr x” and “multiply a b” and we can simply deduce the parameters:

In F#, we define the function prefixed with let and the parameter is separated with white space. This white space is significant, therefore the next identifier after first parameter will the second parameter.
If we have the previous swap function: (also available in F# Tutorial template in Visual Studio)
let swap (a,b) = (b,a)
F# will translate the parameter as Tuples of a and b. And it will also infer the types of a and b as generic.
Recursive functions
Any recursive functions has to be marked with rec keyword after the let keyword.
We already have a recursive factorial sample in the F# tutorial:
let rec factorial n = if n=0 then 1 else n * factorial (n-1)
Again, notice the rec keyword after let.
Function as values (alias delegates in F#)
In all functional programming languages, functions are the same as values. This function as values is the same concept as delegates in .NET. We all know that many LINQ extension methods have delegates as its parameters, and so does F#.
For example: (taken from MSDN Library)
let apply1 (transform : int -> int ) y = transform y
The type of apply1 will be: (using F# interactive)

a function that has parameters of transform function that has int –> int and a y parameter with default type inferred as int, and the body of the function has transform function that takes y as parameter.
We can use the apply1 into these:
let increment x = x + 1
let result1 = apply1 increment 100
Multiple arguments/parameters are separated by “->” sign.
For example:
let apply2 ( f: int -> int -> int) x y = f x y
let mul x y = x * y
let result2 = apply2 mul 10 20
Now we can apply mul function because it has the same signature as f, int –> int –> int.
Again, in functional programming world, the last type always means the return value type.
do Bindings
We can also execute code without function definition or simply executing it independently in F#.
The way we do this in F# by using “do” binding. We can also apply attribute to a do binding.
We can use this techniques to run a code as entry point in a Windows Forms.
A sample usage of F# do binding in a Windows Forms:
open System
open System.Windows.Forms
let form1 = new Form()
form1.Text <- "XYZ"
[<STAThread>]
do
Application.Run(form1)
Lambda Expressions
Now the fun part in F# functions: lambda expressions. The lambda expressions in F# is the same concept as lambda in C# and VB, and prefixed with keyword: “fun”. The purpose of lambda syntax is only for convenience for writing anonymous function (delegate).
A small sample of lambda:
let list = List.map (fun i -> i + 1) [1;2;3]
List.map is conceptually the same as Enumerable.Select in LINQ.
Let’s dive into this lambda deeper!
Now I will use Seq.map to project a collection to another type of collection:
open System.Diagnostics
open System.Linq
let ProcessList = Process.GetProcesses()
let ProcessNames = ProcessList |> Seq.map(fun p -> p.ProcessName)
The Seq.map works conceptually the same as Select in LINQ.
Let’s decompile it! Here’s the layout of the code:

F# compiler will create many compiler generated code. What will ProcessList and ProcessNames look like?
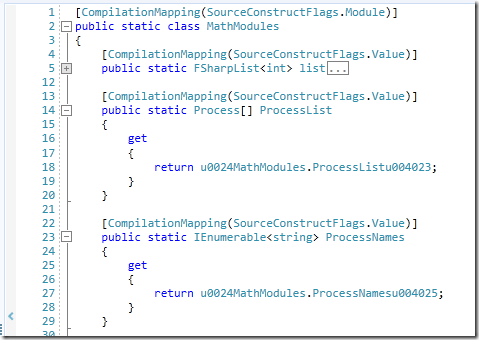
And now let’s dive into the generated u0024.MathModules, we’ll have this:

And the call to Seq.map is available on static constructor of u0024MathModules:
IEnumerable<string> strs = SeqModule.Map<Process, string>(processNamesu004025, (IEnumerable<Process>)processArray);
And you can deduce that any Seq operation actually mapped to SeqModule class with many static functions.
Also List is mapped to ListModule respectively.
Now, where is the content of lambda?
It’s available on ProcessNamesu004025:

Again, delegation in F# is implemented as FSharpFunc internally. And you can see its “p.ProcessName” body is in the Invoke method.
There’s another attribute to hide the other field, the DebuggerBrowsable with parameter DebuggerBrowsableState.Never on it. This also means that this class isn’t meant to be used outside.
Again, this means that F# objects and functions are available for the other programming language as well as long as you don’t have to care the generated code produced by F#.
A gentler introduction to Computation Expressions in F#
A computation workflow is one of F# unique feature comparing to C# and VB. It’s somehow can bring new constructs to your code but it also brings Monad to your everyday use of F#, in a gentler way.
According to F# definition on MSDN Library:
“Computation expressions in F# provide a convenient syntax for writing computations that can be sequenced and combined using control flow constructs and bindings. They can be used to provide a convenient syntax for monads, a functional programming feature that can be used to manage data, control, and side effects in functional programs.”
Now, we can simply assume that F# can do Monad as well! But why it is needed?
As we have discussed before in part 1 and 2, it’s common in functional programming languages to compose functions, not just using it alone or chaining it up (using the “|>” in F#).
This composition comes very handy when you want to construct a DSL or simply encapsulating side effects.
For those outside F#, we can find a sample of Monad in LINQ: the SelectMany! It composes two Func<T,U> and compose it or bind it.
The syntax is:
builder { expression }
The builder is the builder name, and the expression can contain one or more the bang statements (statements that end with !) such as let! and do! statements.
I call them statements, because F# MSDN call them just keywords but this is somehow quite confusing. These keywords need expressions, just like statements in C# and VB.
Then it’s explained further:
“In computation expressions, two forms are available for some common language constructs. You can invoke the variant constructs by using a ! (bang) suffix on certain keywords, such as let!, do!, and so on. These special forms cause certain functions defined in the builder class to replace the ordinary built-in behavior of these operations. These forms resemble the yield! form of the yield keyword that is used in sequence expressions.”
In F#, we already have computation workflow in action: async in asynchronous workflow! More async in part 8.
Here’s the list of methods available for computation expressions:
(taken from http://msdn.microsoft.com/en-us/library/dd233182.aspx )

The most common use is let! keyword. It requires a builder with Bind expression inside of it. The bind will compose two expressions as long as the type is aligned well.
This is the translation from expressions:
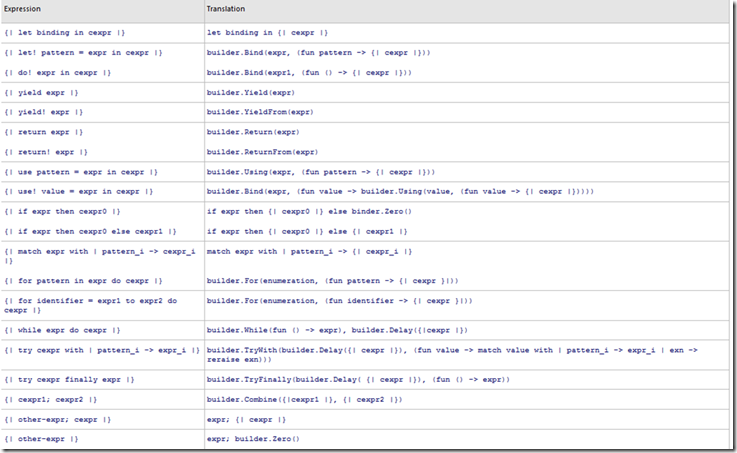
The bind in F# inspired by bind in Haskell, and it’s quite simplified version of Haskell’s but without type classes.
Therefore, this meet the common requirement of Monad: (as explained gently by Wes Dyer in http://blogs.msdn.com/b/wesdyer/archive/2008/01/11/the-marvels-of-monads.aspx blog entry)
- Left identity: Identity.Compose(f) = f
- Right identity: f.Compose(Identity) =f
- Associative: f.Compose(g.Compose(h)) = (f.Compose(g)).Compose(h) and it is equal to “f o g” = f(g(x))
Now we get back to SelectMany:
IEnumerable<TResult> SelectMany<TSource, TResult>( this IEnumerable<TSource> source,
Func<TSource, IEnumerable<TResult>> collectionSelector)
It is the same as bind with this signature:
Bind :: IEnumerable<'T> * ('T –> IEnumerable<'U>) –> IEnumerable<'U>
Abstract that into:
Bind :: M<'T> * ('T -> M<'U>) -> M<'U>
Done, we have monads!
Suppose we want to make Monad for UI. In this sample provided by Adam Granicz from http://www.devx.com/enterprise/Article/40481/0/page/2 we can see the builder for WPF UI:
(I have edited and corrected some type information on the bind)

Using the builder above is simple:
let win =
WindowBuilder()
{ let! panel =
PanelBuilder(StackPanel())
{ let! btn1 = Button(Content = "Hello")
let! btn2 = Button(Content = "World")
return () }
return () }
win.Show() // Pops up the window in FSI.
Run the code in the interactive mode!
I have demonstrated the computation expressions with the twist of OOP in F#. It will be detailed for part 6, OOP in F#.
Next: F# standard libraries in part 5!
Further reference
- Monad in functional programming: http://en.wikipedia.org/wiki/Monad_%28functional_programming%29
- Mathematical Monad: http://en.wikipedia.org/wiki/Monad_(category_theory)
- Adam Granicz article of “Working with DSL and Computation Expression in F#”: http://www.devx.com/enterprise/Article/40481